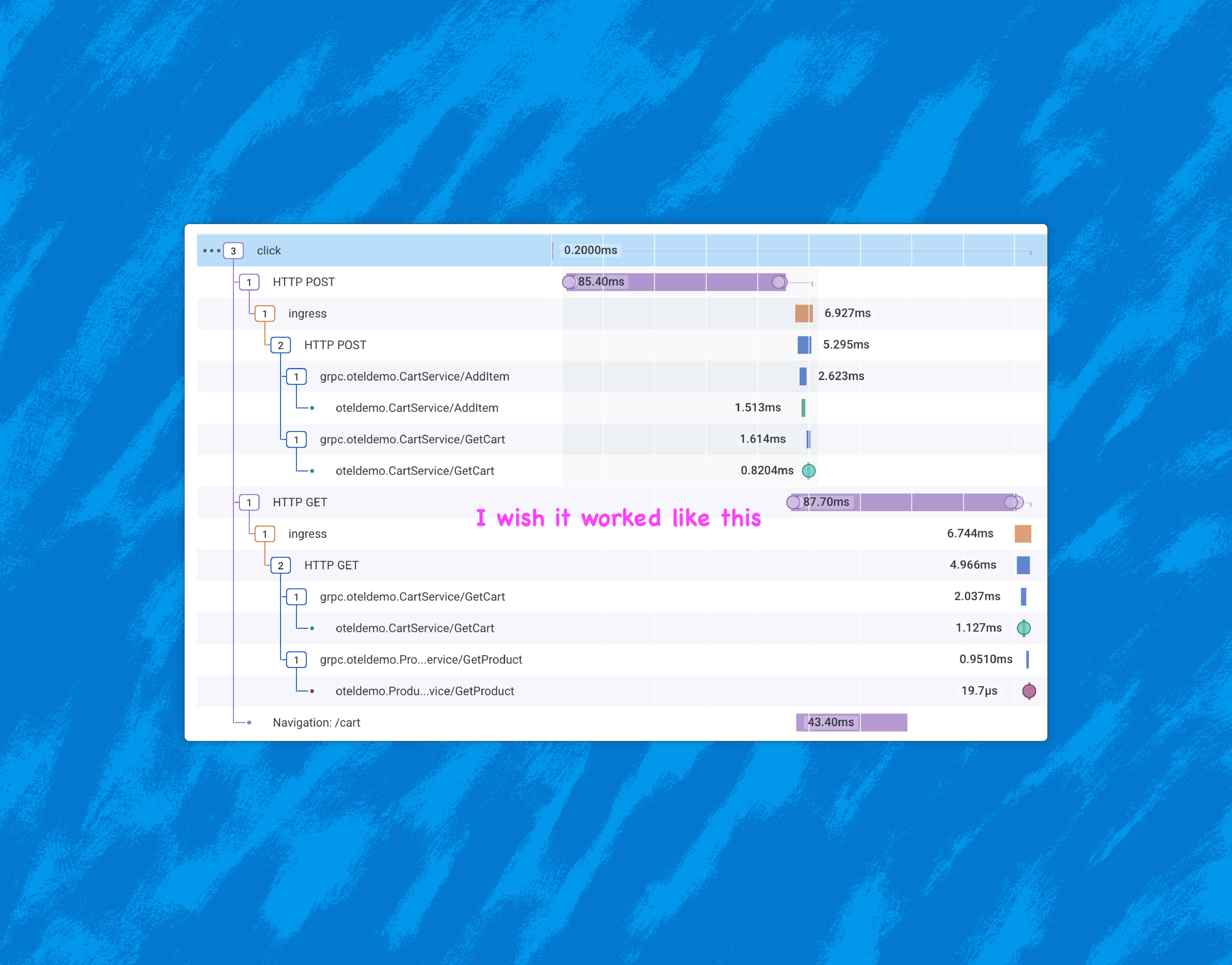
Learn more about Honeycomb Metrics.
In my previous post, we explored why Honeycomb is implemented as a distributed column store. Just as interesting to consider, though, is why Honeycomb is not implemented in other ways. So in this post, we’re going to dive into the topic of time series databases (TSDBs) and why Honeycomb couldn’t be limited to a TSDB implementation.
If you’ve used a traditional metrics dashboard, you’ve used a time series database. Even though metrics are cheap to generate, they were historically quite costly to store. TSDBs are therefore ubiquitous nowadays because they’re specifically optimized for metrics storage. However, there are some things they aren’t designed to handle:
- They can’t effectively store high-cardinality data.
- Write-time aggregation loses the context of the raw data, making it difficult to answer new questions.
- Without data to relate pre-aggregated metrics to each other, your investigations can be led down the wrong path.
In contrast, our distributed column store optimizes for storing raw, high-cardinality data from which you can derive contextual traces. This design is flexible and performant enough that we can support metrics and tracing using the same backend. The same cannot be said of time series databases, though, which are hyper-specialized for a specific type of data.
But you have to know the rules before you can break them. So what makes a TSDB tick? While the details depend on the specific implementation, we’ll focus on Facebook Gorilla, which has been particularly influential. By studying the compression algorithms introduced by the whitepaper, we’ll learn about the fundamental design of TSDBs. This then informs our discussion about the real-world problems with trying to rely on TSDBs for observability.
What is a time series database?
A time series database is a specialized database that efficiently stores and retrieves time-stamped data. Each time series is stored individually as an optimized list of values, enabling fast data retrieval and cost-effective storage.
These databases have been widely used in traditional metrics and monitoring products due to their performance benefits. However, these optimizations come with limitations that hinder their suitability for true observability solutions.
Metrics, time series databases, and Facebook Gorilla
The most basic unit of service monitoring is the metric. Metrics are really just numbers that capture some important piece of information about your environment. They’re particularly useful for system-level diagnostics: CPU utilization percentage, bytes of free memory, number of network packets sent, and so forth. But the idea is so simple that data often gets generated for application-level insights, too: milliseconds of request latency, number of error responses, domain-specific measurements, etc. (As we’ll see, vanilla metrics aren’t actually as useful for this latter type of data.)
Importantly, metrics change over time. You can’t just take one reading of your CPU usage and get a permanent picture of your system’s health. Instead, you want to keep taking readings every so often at a regular collection interval (e.g., every 15 seconds), recording each metric’s value along with the time when it was measured. Storing this data is where time series databases like Prometheus, InfluxDB, and Whisper come into play.
A time series is a sequence of data points where each point is a pair: a timestamp and a numeric value. A time series database stores a separate time series for each metric, allowing you to then query and graph the values over time.
At first glance, this doesn’t seem so complicated. The TSDB could store each point in all of 16 bytes: a 64-bit Unix timestamp and a 64-bit double-precision floating point number. For example, a time series for your CPU stats might look like this:
| Unix timestamp | CPU usage (%) |
| 1600000000 | 35.69 |
| 1600000015 | 34.44 |
| 1600000030 | 32.19 |
| 1600000044 | 53.94 |
| 1600000060 | 37.56 |
The timestamp is an integer number of seconds since the Unix epoch, which naturally increases over time. Here, we can guess there’s a 15-second collection interval, although in the real world there’s bound to be some jitter where the clock will be off a little here or there. The CPU usage is a floating point number that probably hovers around the same value if the system is healthy, but could see dramatic spikes. Other metrics might be representable as integers, but using a floating point type is more general.
However, this simple representation has problems at scale. Not only are metrics prolific, but the sheer number of services generating those metrics in modern distributed systems means that a TSDB may be maintaining millions of active time series at once. Suddenly, those 16 bytes start adding up. Fewer series can be held in memory, so performance suffers as writes and queries have to hit the disk. Then long-term storage becomes more expensive, so less data can be retained.
Thus, a major avenue of optimization for TSDBs is compression, reducing the number of bits needed to represent the same data. Since time series have a very specific structure, we can leverage specialized encodings. In particular, two compression schemes were introduced by Facebook Gorilla that have influenced several other TSDBs, including Prometheus (see this PromCon 2016 talk) and InfluxDB (at least version 1.8). Analyzing these two schemes—one for timestamps, one for values—will give us a general feel for the sorts of problems that TSDBs solve.
Optimizing time series databases
To compress timestamps, the first thing to notice is that they’re always increasing. Once we know the initial timestamp, we know that every subsequent timestamp is offset against the previous one. This gives rise to delta encoding, which stores the differences instead of the raw values. For example, our CPU time series from before has the following deltas for each of its timestamps:
| Unix timestamp | Delta |
| 1600000000 | – |
| 1600000015 | 15 |
| 1600000030 | 15 |
| 1600000044 | 14 |
| 1600000060 | 16 |
We still have to store the first timestamp as a 64-bit integer, but the deltas are far smaller, so we needn’t use as many bits.
But we can go one step further by noticing that the deltas are almost all the same. In fact, due to the periodic nature of metrics, we expect the deltas to be equal to the collection interval (here, 15 seconds). There’s still the possibility of jitter, though, so we can’t just assume the deltas are always going to be the same exact value.
Realizing this, we can compress timestamps even more by applying delta encoding to our delta encoding, giving us a delta-of-deltas encoding:
| Unix timestamp | Delta | Delta of deltas |
| 1600000000 | – | – |
| 1600000015 | 15 | – |
| 1600000030 | 15 | 0 |
| 1600000044 | 14 | -1 |
| 1600000060 | 16 | +2 |
After storing all 64 bits of the first timestamp, then the first delta for the second timestamp, we can just store the delta-of-deltas. Except in cases of jitter, we expect the delta-of-deltas to be 0, which can be stored in a single bit. For Facebook, they found this to be the case for 96% of their timestamps! And even the variances due to jitter are expected to be small, which allows us to achieve an aggressive compression ratio.
A similar strategy can be used for metric values as well. However, we don’t have the same constraints that allow for simple deltas. In principle, subtracting any two arbitrary floats just results in another float, which takes the same number of bits to encode. Instead, we turn to the binary representation of our double-precision floats, as specified by the IEEE 754 standard.
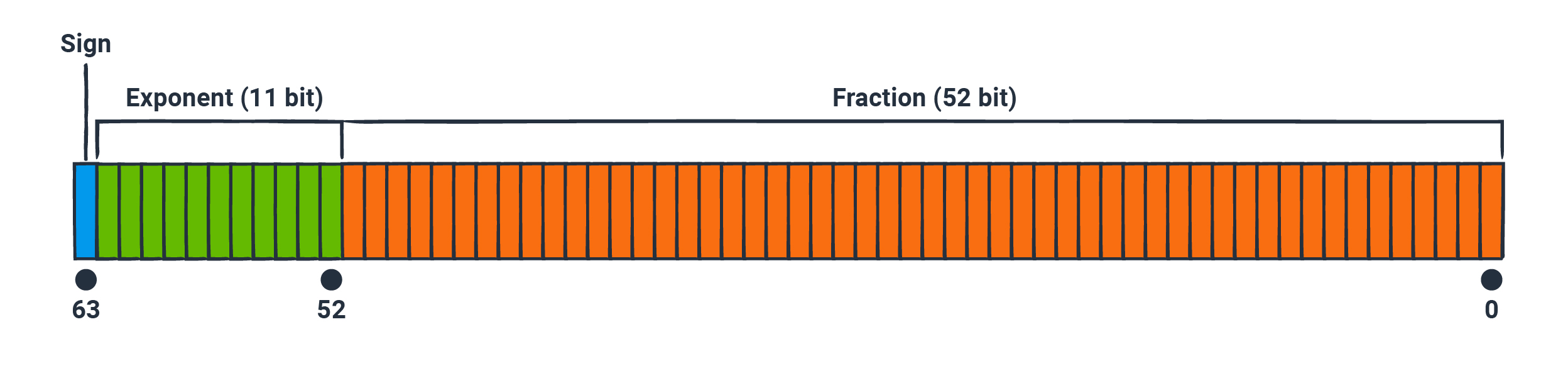
The 64 bits are broken up into three parts: the sign (1 bit), the exponent (11 bits), and the fraction (52 bits). The sign bit tells us whether the number is positive or negative. The exponent and fraction work almost the same way scientific notation does in base 10, where the number 123.456 would have the fractional part of 0.123456 and the exponent of 3, since 0.123456 × 10^3 = 123.456. You can think of the exponent as an order of magnitude, while the fraction is the “payload” of the number.
Within a single time series, it’s reasonably likely that the values are going to have the same sign and order of magnitude, so the first 12 bits are probably the same between measures. For example, CPU usage is always a positive number between 0 and 100. The fractional values might also stay relatively close together, but there’s probably more fluctuation. For instance, the CPU usage might hover around the same narrow band as long as the system is healthy, but it could also spike up or crash down.
Thus, instead of subtracting subsequent values as in delta encoding, we can do a bitwise XOR between successive values. The first 12 bits will often be the same, so their XOR will be zero. There will also be some number of trailing zeroes—more if the binary representations are close together. Using hex notation for the sake of compactness, our example CPU usage metrics have the following XOR results:
| CPU usage (%) | Hex representation | XOR with previous |
| 35.69 |
0x4041d851eb851eb8
|
– |
| 34.44 |
0x40413851eb851eb8
|
0x0000e00000000000
|
| 32.19 |
0x40401851eb851eb8
|
0x0001200000000000
|
| 53.94 |
0x404af851eb851eb8
|
0x000ae00000000000
|
| 37.56 |
0x4042c7ae147ae148
|
0x00083ffffffffff0
|
Why bother with this? Because rather than store all 64 bits of the XOR result, we can use its predictable shape to devise a custom encoding. For instance, consider the value 0x000ae00000000000, which in binary consists of 12 leading zeroes, 7 significant bits (1010111), and 45 trailing zeroes. We can encode each “chunk” separately:
- Instead of writing out the 12 leading zeroes as
000000000000, we can write the number 12 as1100using only 4 bits. - The significant bits have to be written out in full, but the number of bits is variable. So we write the number of significant bits followed by the bits themselves. Here, that’s
111(7) followed by1010111for a total of 10 bits. - The number of trailing zeroes is implied by the information encoded above. We know the full width is 64, and 64 – 12 – 7 = 45. So we needn’t encode anything else for the last chunk.
Thus, instead of 64 bits, we can represent this value in as few as 4 + 10 + 0 = 14 bits. In practice, this isn’t quite the end result. We may need additional bits to delimit the chunks, and there are other tricks to squeeze a couple bits out. However, the overall idea is still the same.
As we can see from the example, though, this compression scheme has more variability. The first three XOR results have a lot of zeroes, so they compress by a lot. The last result still has a lot of leading zeroes, but not so many trailing zeroes, so it compresses less. Ultimately, the overall compression ratio really depends on the individual values of the metric.
Still, by combining the two compression algorithms, the Gorilla database used by Facebook saw data points shrink from 16 bytes to an average of 1.37 bytes! With data that small, more points can fit in memory, leading to faster query performance over longer time ranges. It also means cheaper long-term retention when the values get written to disk.
There are other topics to consider beyond compression, such as efficiently using disk I/O when a time series gets persisted. But this still gives us the crux of what’s being solved by TSDBs: storing a lot of homogeneous, timestamped, numeric data points with as little waste as possible. If you want a taste of more optimization topics, check out Fabian Reinartz’s PromCon 2017 talk, “Storing 16 Bytes at Scale.” For our purposes, though, this understanding gives us a foothold for discussing the use of TSDBs in the wild.
Tagging vs. high cardinality
Now that we can keep track of our data points, let’s consider how they’re actually used. Say we have an e-commerce app written in Python using Flask to serve various API endpoints. A very reasonable application-level metric might be the number of errors users see. Using something like StatsD, we could set up an error handler to increment a metric:
import statsd
stats = statsd.StatsClient()
@app.errorhandler(HTTPException)
def handle_error(e):
stats.incr("errors")
# ...
Under the hood, the StatsD daemon is maintaining a counter of how many errors we’ve seen during the collection interval. At the end of each interval, the value is written out to the errors time series in the TSDB, then the counter is reset to 0. Thus, the counter is really a rate of errors per interval. If we see it trending up, something is probably going wrong.
But what exactly is going wrong? This single counter doesn’t tell us much. It could be some dire bug resulting in HTTP 500 errors, or it could be a broken link in an email campaign leading to increased HTTP 404 errors, or any number of other things. In order to split out this metric, it’s very common for vendors to provide tags or labels—pieces of key-value metadata that can be attached to a time series. While vanilla StatsD doesn’t support tagging, clients like Prometheus do. For instance, we could attach an HTTP status label like so:
from prometheus_client import Counter
errors = Counter("errors", "HTTP exceptions per interval", ["status"])
@app.errorhandler(HTTPException)
def handle_error(e):
errors.labels(e.code).inc()
# ...
Although Prometheus counters work slightly differently from StatsD counters, labels work in fundamentally the same way across TSDBs that support them. Ultimately, the database is going to wind up storing a separate time series for each tag value. So for every possible status code, there will be a distinct time series with its own data points. The errors{status=500} time series will contain different data from the errors{status=404} series, so they can be graphed individually and we can see the respective error rates per status code. The errors series represents the sum of these other ones.
Why stop there, though? The HTTP status code isn’t the only thing that differentiates errors. For our hypothetical e-commerce site, we might tolerate different error rates for the /checkout API than for the /reviews API. We could add another tag for the request path in an effort to get as much context as possible:
from prometheus_client import Counter
errors = Counter("errors", "HTTP exceptions per interval", ["status", "path"])
@app.errorhandler(HTTPException)
def handle_error(e):
errors.labels(e.code, request.path).inc()
# ...
Then the errors{status=500,path=/checkout} time series will be different from the errors{status=500,path=/reviews} series. But it goes beyond that: the TSDB will have to store a separate time series for each unique combination of status and path, including errors{status=404,path=/checkout} and errors{status=404,path=/reviews}. Suppose there are 10 possible error codes and 20 possible API endpoints. Then we would be storing 10 × 20 = 200 different time series.
This isn’t too outrageous yet. There are relatively few possible values for the tags we’ve added thus far. That is, they have low cardinality. However, consider a tag that has high cardinality (many possible values). For instance, a user ID tag could be handy, since error scenarios might only apply to specific users. But the number of user IDs might be very high, depending on how popular the site is. Suppose there are 1,000,000 users. With just these three labels, the TSDB has to store 10 × 20 × 1,000,000 = 200,000,000 different time series. It gets even more dangerous with tags of unbounded cardinality, like HTTP User-Agent strings, which could be anything.
TSDBs are good at what they do, but high cardinality is not built into the design. The wrong tag (or simply having too many tags) leads to a combinatorial explosion of storage requirements. This is why vendors will typically charge based on tag counts, or even cap certain plans at a limited number of value combinations. With a TSDB, you’re not able to label metrics based on some of the most important differentiators. Instead, you have to work with coarse-grained data, using at best a handful of low-cardinality tags.
Aggregation vs. raw data
While tags can make a time series database store too much data, there are also ways in which TSDBs won’t store enough data. This has to do with how metrics get generated.
Suppose we’ve had performance issues in the past linked to users with large cart sizes—that is, the number of items users have at checkout. It would be reasonable to track a metric for this, in case we run into the same issue again. But we wouldn’t be able to use a counter like before since the cart size isn’t cumulative. Different users have different cart sizes at different times, even within a single collection interval. Suppose we have a 30-second collection interval and we see the following checkouts during the 1600000000 – 1600000030 interval:
| Timestamp | Cart size |
| 1600000003 | 3 |
| 1600000007 | 14 |
| 1600000010 | 15 |
| 1600000011 | 9 |
| 1600000017 | 26 |
| 1600000017 | 5 |
| 1600000026 | 3 |
These are technically timestamped numbers, but they all happen at different times that are spread out in an unpredictable distribution (perhaps even concurrently). Because the TSDB relies on the regularity of the time deltas, we want to wait until the end of the collection interval to write a single number to the time series. That is, we need an aggregate number that somehow represents the totality of the data points. A counter is one type of aggregate where the values are summed. But this doesn’t tell us how many items a typical user purchases. Instead, we’d probably choose to record the average cart size per interval.
To track such metrics, it’s common for libraries to provide a histogram function:
@app.route("/checkout")
def checkout():
cart = get_cart()
stats.histogram("cart_size", len(cart))
# ...
Broadly speaking, the client will maintain a list of the cart sizes during each collection interval. At the end of an interval, aggregates get computed from that list and written to the TSDB, then the list is cleared for the next interval. Each aggregate goes in its own time series. They might include:
cart_size.sum= 75cart_size.count= 7cart_size.avg= 10.71cart_size.median= 9cart_size.p95= 22.7cart_size.min= 3cart_size.max= 26
But no matter which aggregate we’re computing, the fact remains that we’re throwing away the original data points at write time. You’ll never be able to read them back. For instance, while you could see the average cart size is 10.71, the data points could just as well have been [3, 14, 15, 9, 26, 5, 3] or [10, 8, 8, 13, 13, 13, 10] or [7, 11, 12, 16, 16, 9, 4] or any number of other possibilities. There are additional aggregates you could compute in addition to the average to try to get a clearer picture, such as the standard deviation. But at the end of the day, the only way to get full resolution is to have the raw data on hand, which isn’t amenable to being stored in the TSDB.
This might not matter for metrics you know you want ahead of time. We wanted the average, so we’re recording the average. But it definitely matters when someone asks a question you didn’t anticipate. Let’s say we see the cart size average hovering around 10, but we still had an outage associated with large carts. How large is “large”? That is, what’s the average size of only the carts above 10 items? How many outliers are there with more than 20 items? Is the average being dragged down by people with especially small carts of only 1 or 2 items? And so on.
None of these questions can be answered based on the averages we’ve been saving to the database. We threw away the original raw data, so we can’t back-calculate. The only thing to do is conjure up a new metric for data going forward. This puts us into a reactive pattern, constantly at the whim of unknown unknowns. Odds are that no one is going to have the foresight to save just the right aggregate that will let us answer these important questions about cart sizes, let alone debug some novel new failure mode when we get paged in the middle of the night.
Correlation vs. observability
Let’s picture such a failure scenario. Say it’s Black Friday, the biggest day of the year for our e-commerce site. By the middle of the day, alerts start going off. That’s okay; it’s why we have the proactive alarms wired up to our errors time series. So we get to troubleshooting and open up the metrics dashboard.
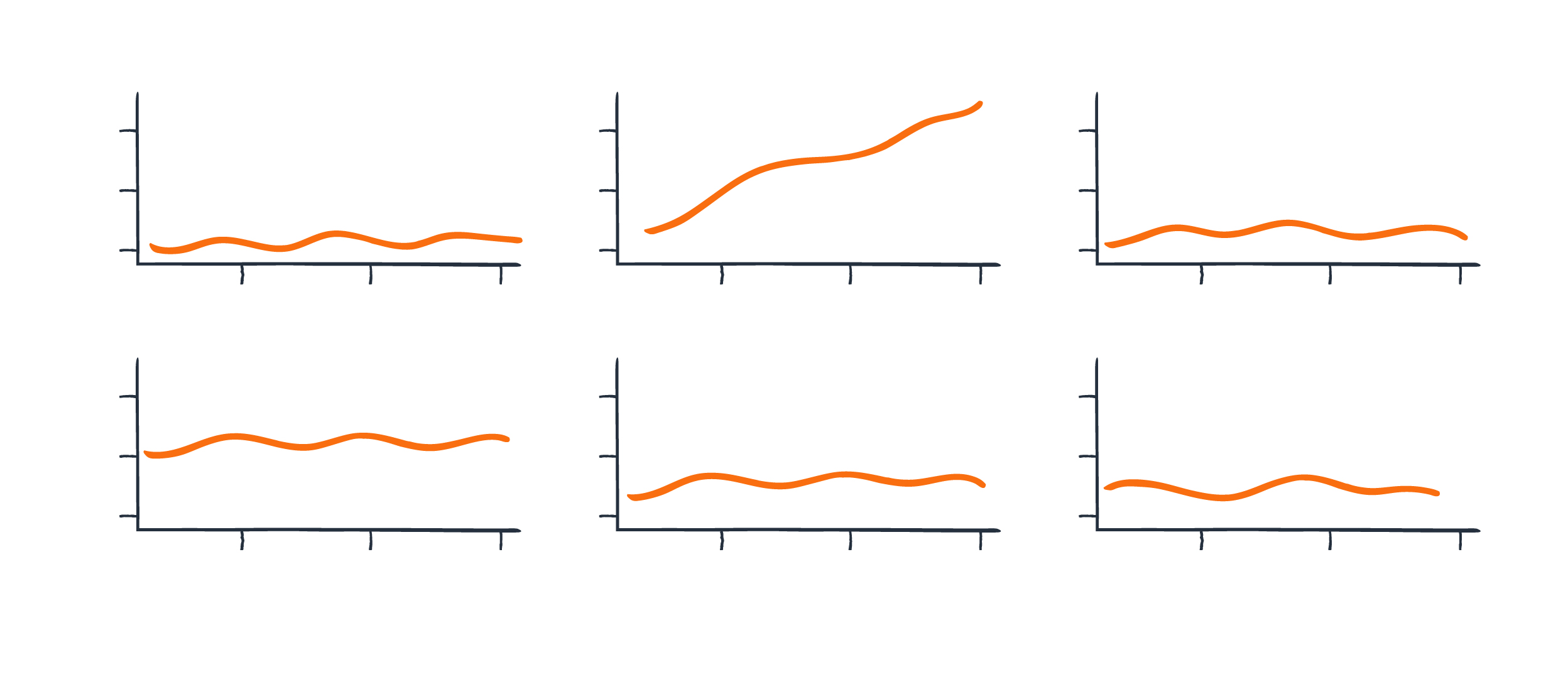
Sure enough, the graph is showing an uncomfortable increase in HTTP 500 errors on the /checkout API. What could be causing it? Well, we’ve seen performance issues with cart sizes before. It seems reasonable that this problematic code might result in errors, so we consult the cart_size.avg time series to check.
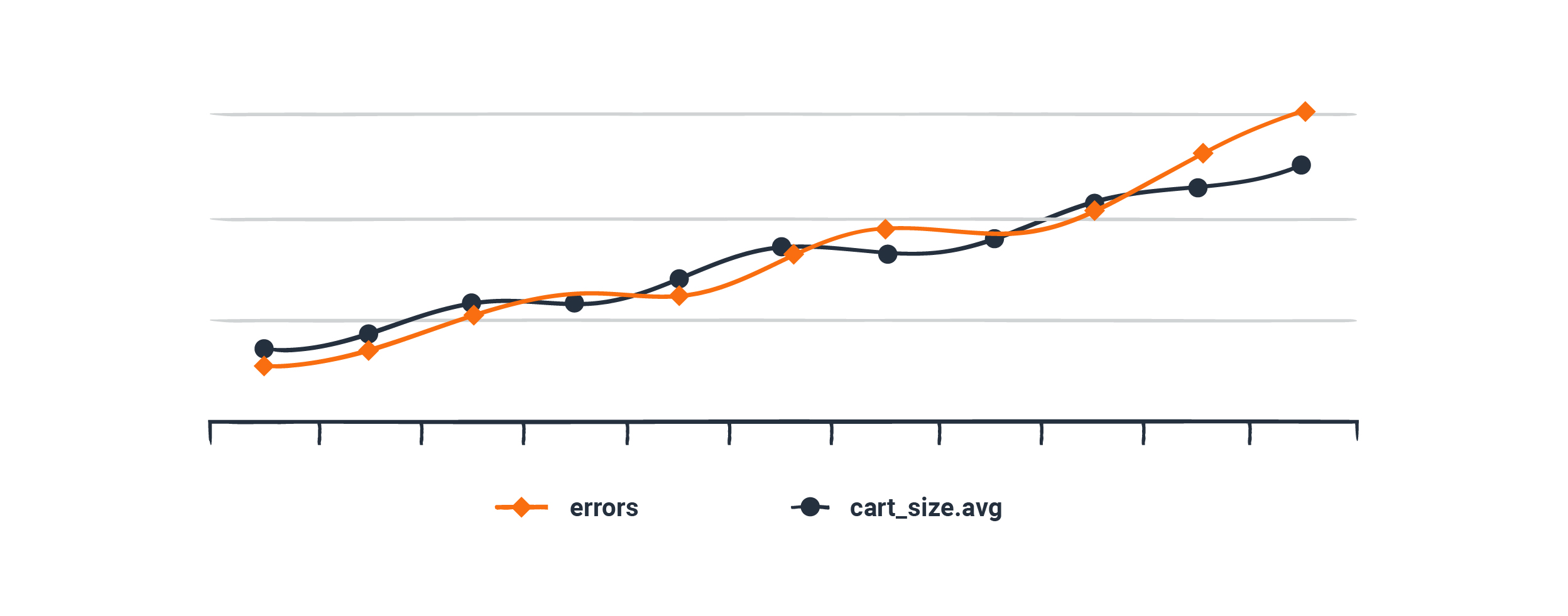
Comparing it to the errors{status=500,path=/checkout} series, it looks like the cart size and the error rates are rising in lockstep, which seems awfully suspicious. Hypothesis in hand, we set out to reproduce a scenario where a large cart triggers some sort of error.
Except this reasoning is flawed. We could waste an hour digging into this rabbit hole before a customer support ticket comes in that users can’t apply a specific coupon code at checkout—an error that has nothing to do with the cart size. Cart sizes are just trending up because it’s Black Friday, and the errors happen to be increasing at the same time due to a special Black Friday coupon code that is broken.
As they say, correlation does not imply causation. Humans are pretty good at pattern-matching, even when the pattern is coincidental. So when we squint at the graphs and try to line things up, our brains might find a spurious correlation. For instance, you may have heard the one that global warming is caused by a lack of pirates. After all, as the number of pirates has trended down, the average global temperature has trended up!
Not every correlation is a bad one, of course. Yet we still risk chasing these red herrings because TSDBs lack the proper context—a flaw imposed by their own design. We can’t tag the errors with the coupon codes that users submit because the cardinality of text input is virtually unbounded. We also can’t drill down into the aggregates to find an individual data point telling us that errors still occurred at small cart sizes.
This example has illustrated an overall lack of observability: the ability to infer the inner workings of your system by what you see on the outside. That’s why, in trying to solve for observability, Honeycomb couldn’t be limited to a TSDB implementation.
Honeycomb is different
A lot of work has gone into making time series databases very good at what they do. Metrics are always going to be cheap to generate, and with the power of a TSDB, you’ll be able to easily chart aggregate trends over long periods of time. But when it comes to observability, there are several ways in which numeric time series data just won’t capture enough context.
This is what motivated the design of Honeycomb’s backend, which optimizes for storing raw data and making queries fast. So in the areas where TSDBs are lacking, the distributed column store really shines:
- Storage requirements are not dependent on the cardinality of your data. Therefore, you can attach high-cardinality fields to your events at no additional cost.
- Raw data is stored at write time, and aggregates are only computed at query time. Nothing is thrown away, giving you the ability to chart the coarse-grained aggregates as well as drill down into the fine-grained data points.
- By organizing your data relationally into traces, you no longer have to rely on correlating disparate graphs in an attempt to observe the behavior of your system.
Plus, we can derive metrics from wide events, whereas wide events cannot be derived from metrics. True, Honeycomb won’t be as good at compressing individual time series the way a TSDB does. But instead, we can package together all the metrics at the end of each collection interval and write them as one row in our column store:
timestamp
|
cpu
|
mem_used
|
mem_free
|
net_in
|
net_out
|
...
|
| … | … | … | … | … | … | … |
Because tracing already gives you so much context, you’ll probably find yourself relying less on metrics for application-level behavior. Still, metrics are useful for systems-level diagnostics to understand if your machines are healthy, plan for infrastructure capacity, and so on. So it’s worth having a backend that supports both tracing and metrics.
The point isn’t that TSDBs are bad and column stores are good. As ever, engineering is about trade-offs. But now that we’ve seen how TSDBs work, as well as how they don’t, we can make our decisions with a better understanding of what those trade-offs are. If you’d like to learn more, check out our docs on Honeycomb Metrics. Get started with Honeycomb Metrics with a free Enterprise account trial!